Berücksichtigung der Luftblasendynamik in Niederdruck-Hydrauliksystemen

Rohrresonanzen und andere Schwingungsphänomene in hydraulischen Systemen werden stark von der Schallgeschwindigkeit im Druckmedium beeinflusst. Um bei der CAE-gestützten Systemauslegung oder simulationsgestützten Fehlersuche das ursprüngliche Systemverhalten möglichst genau reproduzieren zu können, muss die Schallgeschwindigkeit in den einzelnen Komponenten genau bekannt sein. Diese Größe wird unter anderem durch die Luftblasen im Druckmedium beeinflusst, deren dynamische Effekte bisher nicht berücksichtigt wurden.

In einem vom Bundesministerium für Wirtschaft, Mittelstand und Energie (BMWi) geförderten Forschungsprojekt entwickelt FLUIDON in Zusammenarbeit mit dem renommierten Institut für fluidtechnische Antriebe und Systeme (ifas) der RWTH Aachen ein Berechnungsverfahren, um diese Effekte in der hydraulischen Simulation mit DSHplus abdecken zu können.

Projekthintergrund und -absicht

Die Schallgeschwindigkeit in einer hydraulischen Komponente wird von den folgenden Einflussgrößen bestimmt:

• Steifigkeit der Druckflüssigkeit (druck- und temperaturabhängig)

• Steifigkeit der Bauteilwandung

• Steifigkeit ungelöster Luftanteile (insbesondere im Niederdruckbereich!)

Infolge der niedrigen Steifigkeit der Gasblasen kann die Schallgeschwindigkeit des Flüssigkeit-Luft-Gemischs mitunter um mehr als eine Größenordnung geringer als die der reinen Flüssigkeit ausfallen. Bisher wird der Einfluss der Gasblasen auf die Gemischsteifigkeit bei praktisch allen marktüblichen Softwarelösungen lediglich durch einen quasistatischen Berechnungsansatz berücksichtigt. Dabei wird davon ausgegangen, dass die einzelnen Luftblasen zu einem einzigen Gasvolumen zusammengefasst werden können, welches sich wie eine ideal-elastische Feder verhält.

Wie Experimente zeigen, ist diese Annahme nur für Schwingungen mit sehr niedriger Frequenz zulässig. Bei größerer Dynamik muss berücksichtigt werden, dass die Gasblasen bei Größenänderungen die umliegenden Flüssigkeitsteilchen verdrängen und deren innere Reibung überwinden müssen, sodass die effektive Steifigkeit der Gasblasen frequenzabhängig wird.

Da für die dynamischen Effekte die Größe der Blasen (und damit die Menge der beteiligten Flüssigkeitsteilchen) ebenfalls von Bedeutung ist, werden Anzahl und Durchmesser der einzelnen Blasen in Form einer statistischen Häufigkeitsverteilung erfasst. Zur effizienten Berechnung werden die verschiedenen Blasengrößen in Größenklassen („Cluster“) zusammengefasst.

Erstes wichtiges Zwischenergebnis des Forschungsprojekts ist eine Gleichung zur Berechnung der zeit- und frequenzabhängigen Schallgeschwindigkeit des Flüssigkeits-Luft-Gemischs, wobei die Blasendynamik durch die sog. Rayleigh-Plesset-Gleichung (RPG) modelliert wird.

Frequenzgang der Schallgeschwindigkeit eines Flüssigkeits-Gas-Gemischs mit nur einer Blasengröße

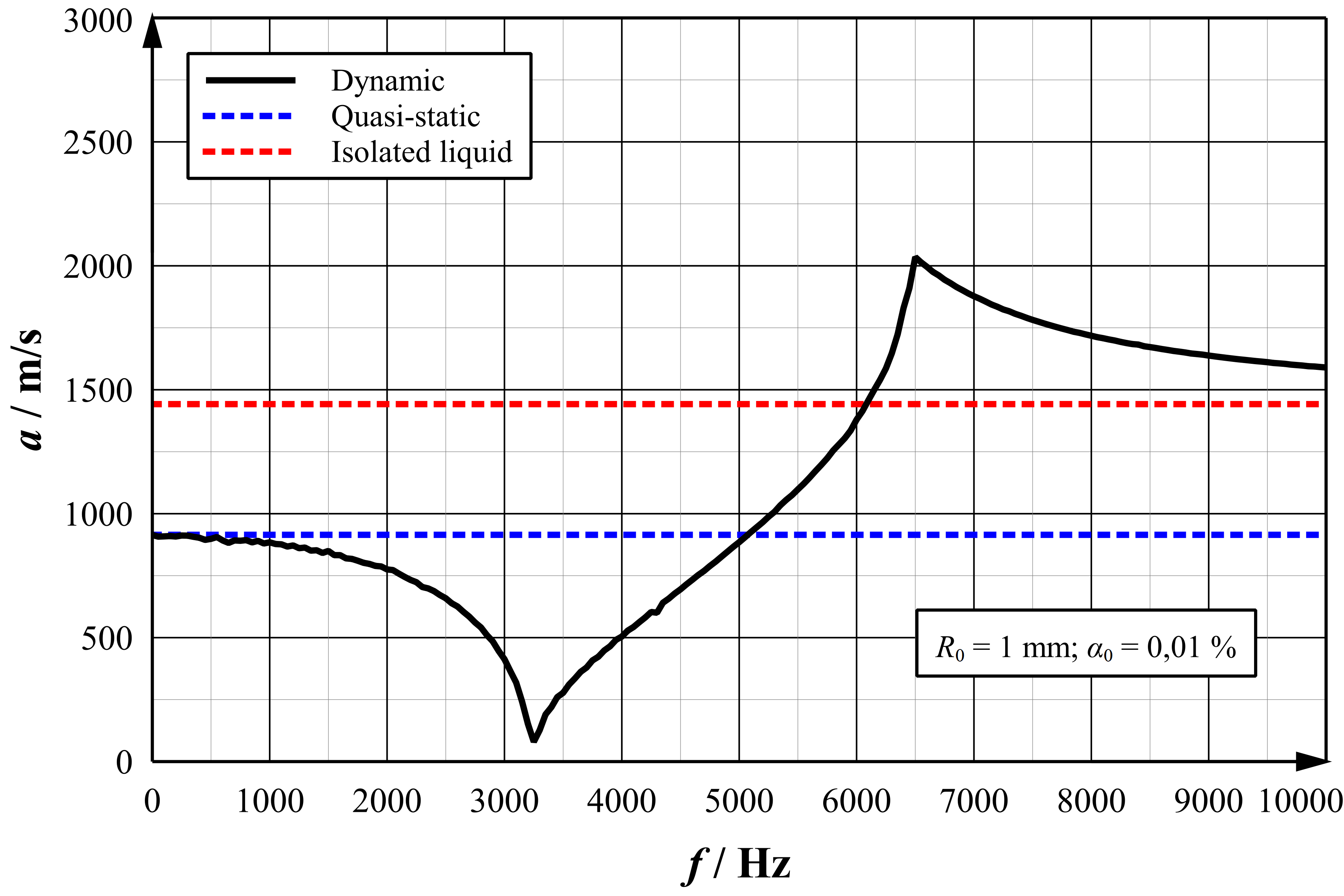
Der Frequenzgang der nach dieser Methode berechneten Schallgeschwindigkeit ist für ein beispielhaft ausgewähltes Gemisch mit einer Blasengröße in der nebenstehenden Abbildung dargestellt.

Die Schallgeschwindigkeit des Flüssigkeits-Gas-Gemischs geht für verschwindend geringe Frequenzen in die quasi-stationäre Lösung unter Vernachlässigung der Blasendynamik (bisheriger Stand der Technik) über. Das ausgeprägte Minimum (hier: 3200 Hz) der Schallgeschwindigkeit korrespondiert mit der Resonanzfrequenz der Blasengröße; die effektive Steifigkeit der Gasblase ist aufgrund der Trägheitskräfte bei dieser Frequenz besonders gering.
Da die durch die RPG modellierten Trägheitskräfte bei großen Frequenzen zu einer Versteifung der Blasen führen, verbleibt in diesem Bereich nur die Kompressibilität der Flüssigkeit, sodass die Gemisch-Schallgeschwindigkeit gegen die der isolierten Flüssigkeit strebt.

Frequenzgang der Schallgeschwindigkeit eines Flüssigkeits-Gas-Gemischs mit unterschiedlichen Blasengrößen

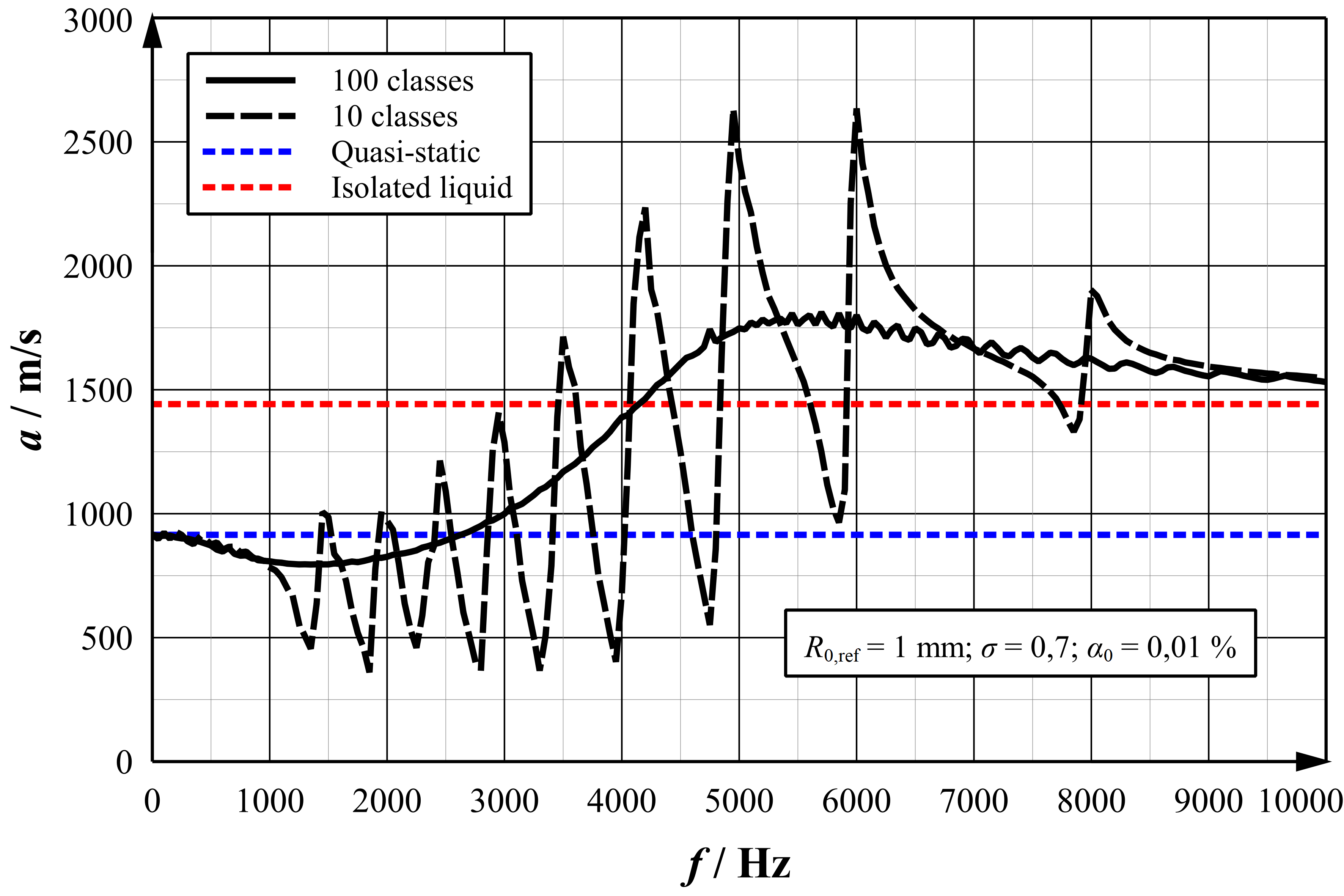
Eine entsprechende Rechnung für ein Gemisch mit einer Blasenverteilung ist in der nebenstehenden Abbildung gezeigt.

Zur Verdeutlichung des Einflusses der Clustergröße wurden die Frequenzgänge für 10 und 100 Klassen berechnet. Die ausgeprägten Minima im Frequenzgang für 10 Klassen entsprechen den Resonanzfrequenzen der einzelnen Blasengrößen. Die Maxima und Minima sind bei 100 Klassen deutlich weniger scharf abgegrenzt, da die Häufigkeit (und damit der Volumenanteil) der einzelnen Blasengrößen bei einer größeren Klassenanzahl entsprechend geringer ausfällt.

Der Frequenzgang für 100 Klassen ist von der (hier nicht dargestellten) kontinuierlichen Lösung praktisch nicht unterscheidbar.

Das entwickelte Rechenschema wird derzeit in das bewährte Charakteristikenverfahren zur Leitungsberechnung eingebunden.