Im Gegensatz zu den reibungsbedingten Druckverlusten entlang einer Rohrleitung entstehen diskrete Druckverluste durch lokale Störungen des Strömungsprofils. Diese Störungen führen zu Energieverlusten, die sich in Form von Druckabfällen bemerkbar machen und die Effizienz des Systems erheblich beeinflussen können.
Solche lokalen Druckverluste treten insbesondere an strömungstechnischen Engstellen auf, die durch eine oder mehrere der folgenden Ursachen entstehen:
- Änderung der Querschnittsfläche – z. B. bei plötzlichen Erweiterungen oder Verengungen, die zu Turbulenzen oder Rückströmungen führen.
- Änderung der Strömungsrichtung – insbesondere in Bögen, Umlenkungen oder Verzweigungen, die zusätzliche Strömungswiderstände erzeugen.
- Änderung der Querschnittsform – wie sie beispielsweise in Ventilen, Düsen oder abrupten Übergängen vorkommt und die Strömungsverteilung beeinflusst.
Die DSHplus Piping Systems Library ermöglicht eine detaillierte Simulation dieser diskreten Druckverluste, indem sie die relevanten Effekte in ihren Verbinderbauteilen berücksichtigt. Durch die realitätsnahe Modellierung dieser lokalen Widerstände können Ingenieure mit DSHplus die Strömungseigenschaften optimieren, kritische Druckverluste minimieren und damit die Energieeffizienz des Gesamtsystems verbessern.
Mit der präzisen Berechnung dieser lokalen Strömungswiderstände bietet DSHplus eine leistungsstarke Lösung für die Simulation und Optimierung fluidtechnischer Systeme, von einfachen Rohrleitungen bis hin zu hochkomplexen Netzen mit vielfältigen Strömungsänderungen.
Trotz der Unterschiedlichkeit der vorgestellten Mechanismen erfolgt die mathematische Modellierung der durch sie verursachten Druckverluste in einer einheitlichen Weise, und zwar in Form des Druckverlustbeiwerts \(\zeta\). Der Druckverlustbeiwert entspricht der auf den dynamischen Druck \(\frac{\rho}{2}\bar{u}^2\) bezogenen Differenz der statischen Drücke vor (\(p_1\)) und nach (\(p_2\)) der Störung:
$$\zeta = \frac{p_1-p_2}{\frac{\rho}{2}\bar{u}^2_1}$$
Im Allgemeinen hängt der Druckverlustbeiwert sowohl von der Reynoldszahl \(Re\) als auch von der relativen Oberflächenrauheit \(\varepsilon/D\) ab, wobei die letztgenannte Abhängigkeit von vielen Autoren nicht berücksichtigt wird.
Wie im Folgenden gezeigt wird, entspricht die Druckdifferenz \(p_1 - p_2\) nur für den Spezialfall gleicher Ein- und Austrittsquerschnitte \(A_1 = A_2\) dem Druckverlust \(\Delta p\). Im Allgemeinen ist der Druckverlust als die Differenz der statischen (\(p\)) und dynamischen Drücke (\(q = \rho \bar{u}^2 / 2\)) vor und nach der Störung definiert:
$$\Delta p = p_1 - p_2 + q_1 - q_2 $$
Für den hier betrachteten Fall einer inkompressiblen Strömung bleibt die Dichte auch bei Druckänderungen konstant und kann aus den dynamischen Drücken herausgelöst werden:
$$\Delta p = p_1 - p_2 + \frac{\rho}{2}\left(\bar{u}^2_1 -\bar{u}^2_2\right)$$
Mit der Kontinuitätsgleichung lässt sich die Geschwindigkeit \(\bar{u}_2\) nach der Störung durch die Geschwindigkeit vor der Störung ausdrücken:
$$\bar{u}_2 = \bar{u}_1 \frac{A_1}{A_2}$$
Damit ergibt sich für den Druckverlust:
$$\Delta p = p_1 - p_2 + \frac{\rho}{2}\bar{u}^2_1\left[1-\left(\frac{A_1}{A_2}\right)^2\right]$$
Für den Spezialfall, dass der durchströmte Querschnitt vor und nach der Störung gleich ist (\(A_1 /A_2 = 1\)) vereinfacht sich die Definitionsgleichung des Druckverlusts zu:
$$\Delta p = p_1 - p_2$$
Druckverlust bei Änderung der durchströmten Querschnittsfläche
Bei Veränderung der durchströmten Querschnittsfläche ändert sich neben dem statischen Druck \(p\) auch die querschnittsgemittelte Strömungsgeschwindigkeit \(\bar{u}\), sodass die allgemeine Form der Definition des Druckverlusts verwendet werden muss.
Zunächst wird der Fall einer plötzlichen Querschnittserweiterung betrachtet (\(A_1 < A_2\)), wobei die miteinander verbundenen Rohre einen kreisförmigen Querschnitt besitzen sollen (\(A = \pi D^2 / 4\)).
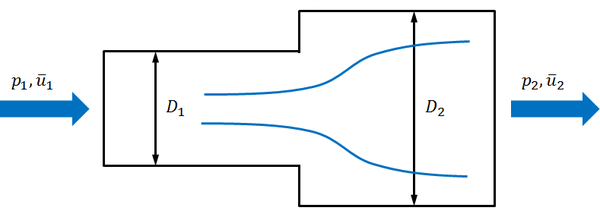
Für diese spezielle Anordnung ist in der Literatur der Begriff des "Borda-Carnotschen Stoßdiffusors" geläufig. Nimmt man an, dass die Druckverluste durch Wandschubspannungen gegenüber den durch Wirbelbildung auftretenden Druckverlusten vernachlässigbar sind, so kann der Druckverlustbeiwert für diesen Spezialfall theoretisch berechnet werden. Durch Kombination von Kontinuitäts-, Impuls- und Energiegleichung ergibt sich ein Gleichungssystem, dessen Lösung den Druckverlustbeiwert \(\zeta\) ergibt [1]:
$$\zeta = \left(1-\frac{A_1}{A_2}\right)^2$$
In der folgenden Abbildung ist der so berechnete Druckverlustbeiwert über dem Durchmesserverhältnis \(D_1/D_2 = \sqrt{A_1/A_2}\) dargestellt:
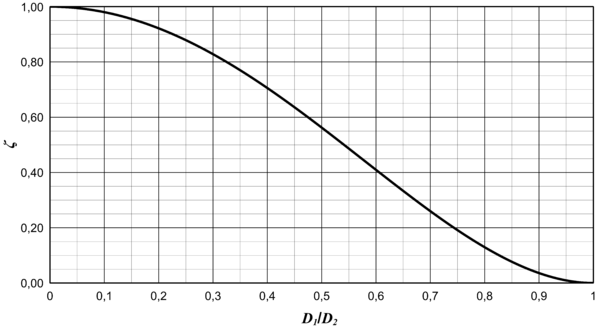
Der umgekehrte Fall entspricht einer plötzlichen Querschnittserweiterung (\(A_1 > A_2\)):
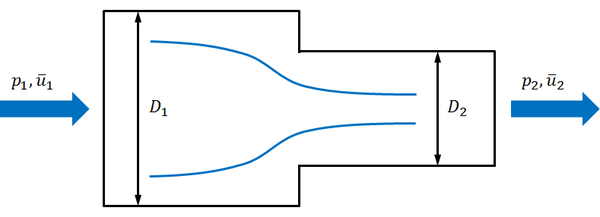
Hier kann keine rein theoretische Lösung angegeben werden, da der für den Druckverlust wesentliche Zusammenhang zwischen Strahlkontraktion und Flächenverhältnis \(A_1/A_2\) nicht bekannt ist. Dieser Zusammenhang lässt sich jedoch experimentell ermitteln, womit sich für kreisförmige Rohre der Druckverlustbeiwert \(\zeta\) nach der folgenden Gleichung ergibt [1]:
$$\zeta = 0,578 + 0,395\beta - 4,538\beta^2 + 14,243\beta^3 - 19,222\beta^4 + 8,540\beta^5 $$
Dabei bezeichnet \(\beta\) das Verhältnis der Durchmesser vor und hinter der Verengung:
$$\beta = \frac{D_2}{D_1}$$
Der Verlauf des Druckverlustbeiwerts für den Fall der plötzlichen Querschnittsverengung ist in der folgenden Abbildung dargestellt:

Druckverlust bei Änderung der Strömungsrichtung
Änderungen der Strömungsrichtung treten beispielsweise bei Krümmern oder Kniestücken auf. Vorausgesetzt, dass die Ein- und Austrittsquerschnitte gleich groß sind, ergibt sich der Druckverlust bei Bauteilen mit Richtungsänderung zu:
$$\Delta p = p_1 - p_2 = \zeta q_1$$
Der Druckverlustbeiwert \(\zeta\) kann der einschlägigen Literatur entnommen werden. Im Lehrbuch von WILL & GEBHARDT [2] ist eine Vorschrift zur Ermittlung von Druckverlustbeiwerterten von gekrümmten Rohren mit Kreisquerschnitt für relative Krümmungsradien \(2<R/D<10\) angegeben. Für die Abhängigkeit des Druckverlustbeiwertes von der Reynoldszahl \(Re\) wird von den Autoren der folgende Ansatz vorgeschlagen:
$$\zeta = \frac{K_1}{Re} + K_2$$
Dabei entspricht \(K_2\) dem Grenzwert des Druckverlustbeiwerts für \(Re \to \infty\). Die Konstanten \(K_1\) und \(K_2\) können den folgenden Tabelle entnommen werden:
| \(R/D\) | \(K_1\) | \(K_2\) |
| 2 | 347 | 0,12 |
| 4 | 448 | 0,22 |
| 6 | 696 | 0,28 |
| 10 | 1154 | 0,43 |
Alternativ können auch die folgenden, von FLUIDON ermittelten Interpolationsformeln zur Ermittlung der Konstanten verwendet werden:
$$K_1 = 1406,50 - \frac{1069,36}{1+\left(\frac{R/D}{7,24}\right)^{3,64}}$$
$$K_2 = -0,0575 + 0,114375\delta - 0,014375\delta^2 + 0,00078125\delta^3$$
Literatur
[1] TRUCKENBRODT, E. Fluidmechanik. Bd. 1: Grundlagen und elementare Strömungsvorgänge dichtebeständiger Fluide. 1980.
[2] WILL, Dieter, et al. Druckflüssigkeiten. Hydraulik: Grundlagen, Komponenten, Schaltungen, 2011, S. 13-40.
