Thermo-hydraulische Simulation mit der DSHplus Piping Systems Library

Die DSHplus Piping Systems Library bietet ein hochentwickeltes Berechnungsmodell, das das temperaturabhängige Verhalten von flüssigen und gasförmigen Medien beim Strömen durch ein komplexes Rohrleitungsnetz präzise beschreibt. Dieses Modell berücksichtigt nicht nur den Wärmeaustausch mit der Umgebung, sondern auch die druck- und temperaturabhängigen physikalischen Eigenschaften des Fluids, um eine realistische und genaue Darstellung der thermischen Strömungsdynamik zu gewährleisten.

Durch die Lösung der thermo-hydraulischen Grundgleichungen ermöglicht die Simulation die Vorhersage von transienten Druckverlusten, Fluidtemperaturen und Durchflussraten an jedem Punkt des Systems. Ingenieure erhalten dadurch wertvolle Einblicke, wie sich das System unter veränderten thermischen und hydraulischen Bedingungen verhält, was eine fundierte Leistungsbewertung und Optimierung ermöglicht.

Einsatzgebiete in Technik und Industrie

Thermo-hydraulische Simulationen werden in vielen Bereichen der Planung und Optimierung von Rohrleitungssystemen eingesetzt. Typische Anwendungen sind:

Kühlkreisläufe in industriellen Maschinen und Kraftwerken, wo eine effiziente Wärmeabfuhr entscheidend ist.
Chemische Prozessanlagen, in denen präzise thermische Bedingungen die Reaktionsführung und Sicherheit beeinflussen.
Energieerzeugungssysteme, wie Dampf- und Gasturbinenkreisläufe, bei denen eine optimierte Wärmeübertragung die Energieeffizienz steigert.
Heizungs-, Lüftungs- und Klimaanlagen (HLK), in denen eine ausgewogene Temperaturverteilung für Energieeffizienz und Komfort sorgt.

Mit DSHplus können Ingenieure die thermischen und hydraulischen Eigenschaften von Rohrleitungssystemen simulieren, analysieren und optimieren, was zu einer höheren Systemeffizienz, reduzierten Energiekosten und einer verbesserten Betriebssicherheit führt. Ob für Forschung, industrielle Anwendungen oder Engineering-Design – DSHplus bietet eine leistungsstarke Lösung zur Bewältigung komplexer thermo-hydraulischer Herausforderungen.

Überblick über die thermo-hydraulischen Funktionen

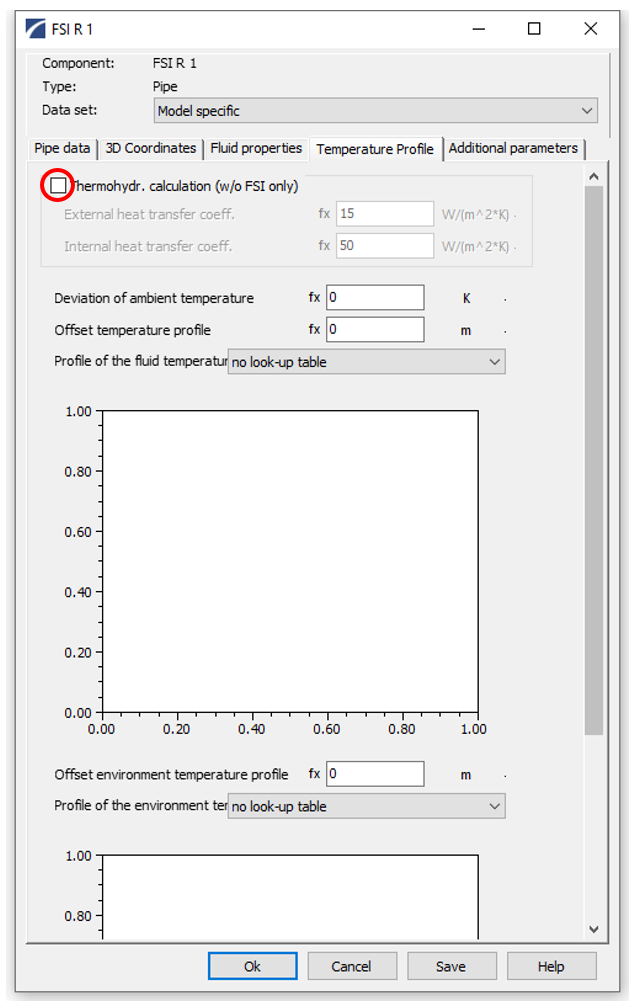
Durch Aktivierung der Option "Thermohydraulische Berechnung" wird das Standard-Gleichungssystem, bestehend aus Impuls- und Kontinuitätsgleichung, um die Energiegleichung erweitert.

Der Wärmestrom kann entweder direkt über die Eingabe "Wärmestrom" vorgegeben werden oder anhand der Wärmeübergangskoeffizienten unter Berücksichtigung der Umgebungstemperatur berechnet werden. Mit der Option "Profil der Umgebungstemperatur" kann der Benutzer eine Verteilung der Umgebungstemperatur angeben.

Der Wärmeübergang zwischen dem Fluid und der Rohrwand sowie zwischen der Rohrwand und der Umgebung wird durch die Parameter "Interner Wärmeübergangskoeffizient" und "Externer Wärmeübergangskoeffizient" beschrieben.

Das mathematische Modell beschreibt die folgenden Phänomene :

Wärmeübertragung zwischen dem Fluid und der Umgebung (Beschreibung über den Wärmedurchgangskoeffizienten)
Dissipative Erwärmung aufgrund von Druckabfall
Druckanstieg in geschlossenen Systemen aufgrund von Temperaturerhöhungen
Der Transport von Energie mit der Strömung (konvektiver Transport)

Das mathematische Modell berücksichtigt derzeit die folgenden Phänomene nicht:

Erhöhung der Wärmeübertragung durch höhere Strömungsgeschwindigkeiten
Druck-, durchfluss- oder temperaturabhängige Wärmeübergangskoeffizienten
Wärmeleitung in axialer Richtung
Wärmekapazität der Rohrwand

Wärmeübertragung zwischen dem Fluid und der Umgebung

Erforderliche Parameter :

Kennfeld für die Umgebungstemperatur Umgebungstemperatur $T_{Env}$-Verteilung oder Einzelparameter, der die Abweichung von der in der Environment-Komponente vorgesehenen Umgebungstemperatur definiert
Innere und äußere Wärmeübergangskoeffizienten
Wärmeleitfähigkeit des Rohrmaterials $k_W$
Wandstärke

Auf der Grundlage dieser Parameter wird der Wärmedurchgangskoeffizient $U$ zwischen der Flüssigkeit und der Umgebung berechnet:

$$U = \frac{1}{\frac{1}{\alpha_i}+\frac{r_i}{k_W}ln(\frac{r_a}{r_i})+\frac{r_i}{\alpha_a r_a}}$$

Die Wärmestromdichte $\dot{q}^"$ (pro Flächeneinheit der inneren Rohroberfläche), der zwischen Flüssigkeit und Umgebung ausgetauscht wird, ist dann gegeben durch:

$$\dot{q}^" = U(T_F-T_{Env})$$

Anwendungsbeispiel der thermo-hydraulischen Simulation

Das System aus drei identischen parallelen Rohren befindet sich zunächst im Ruhezustand und ist auf 20 bar vorgespannt. Die Öltemperatur beträgt 293 K. Die Umgebungstemperatur ist auf 363 K eingestellt.
Innerhalb der ersten 0,5 s wird eine Durchflussrate von 10 l/min erreicht.
Ziel des Versuchs ist es, die drei verschiedenen Möglichkeiten zur Berücksichtigung des Wärmeübergangs durch die Rohrwand bei einer thermo-hydraulischen Simulation darzustellen.

Wärmeübertragung mit festen Wärmeübergangskoeffizienten

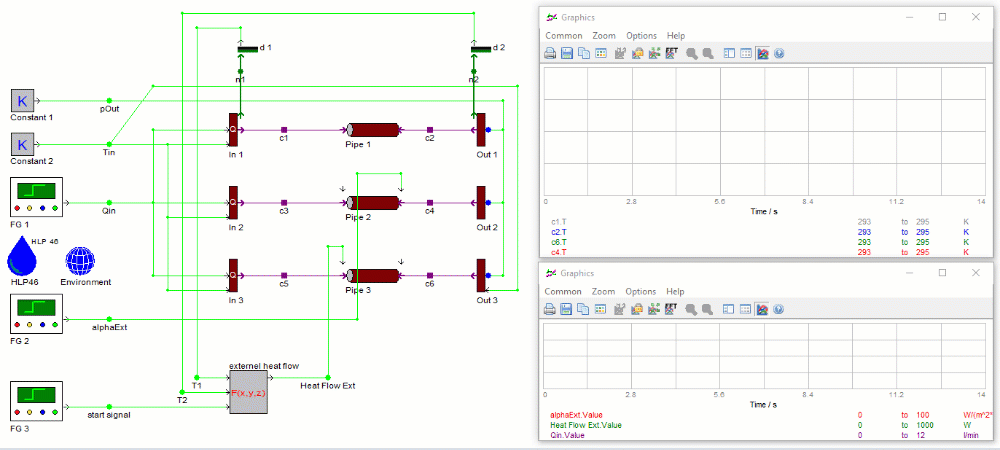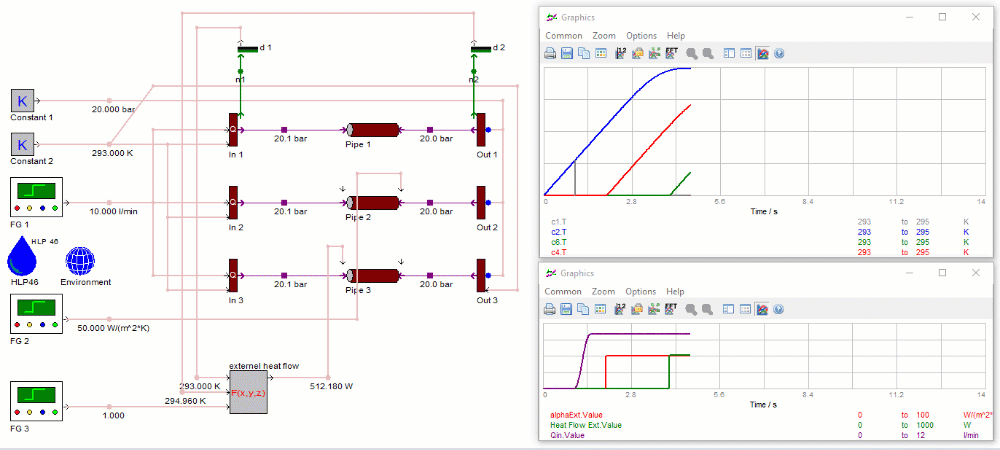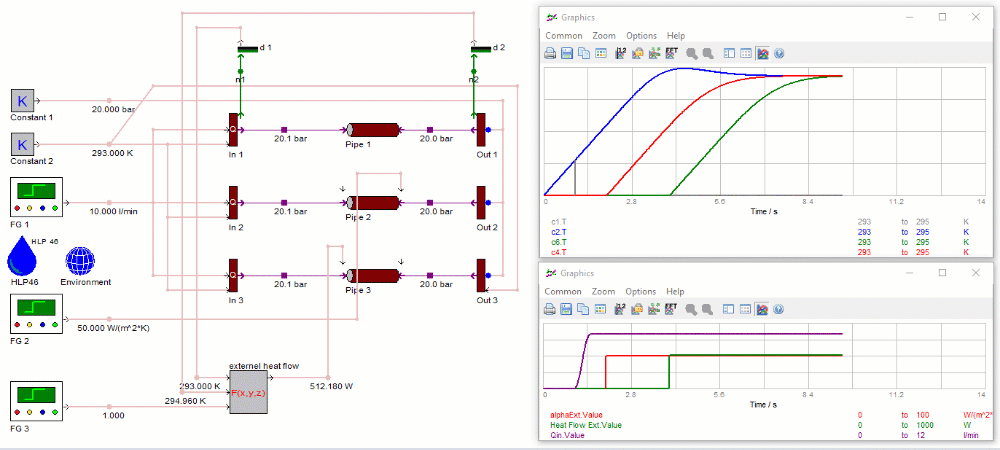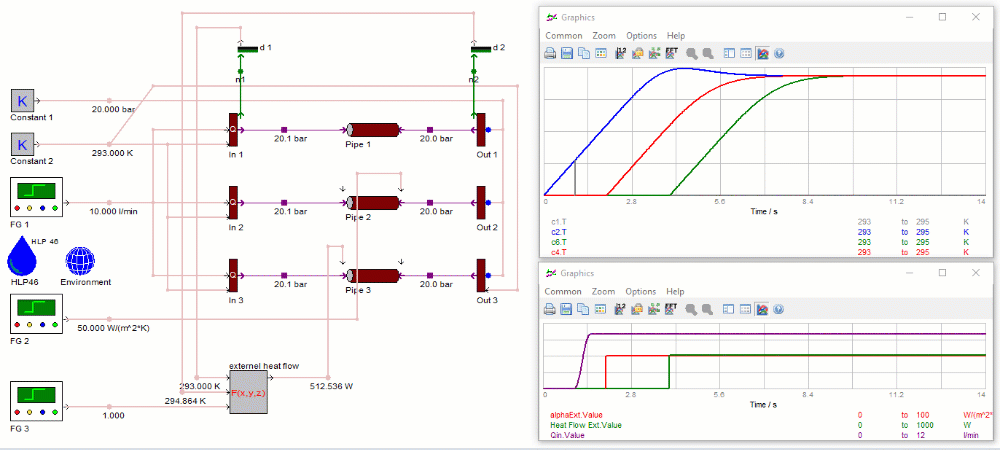
Für das erste Rohr werden die im Dialog parametrierten Wärmeübergangskoeffizienten verwendet. Aufgrund der höheren Umgebungstemperatur kommt es zu einem Nettowärmefluss von der Umgebung durch die Rohrwand zum Öl. Daher steigt die Öltemperatur an beiden Rohrenden (blaue und graue Temperaturkurve in der oberen Abbildung) zu Beginn der Simulation an. Mit Beginn des Ölflusses nach 1 s tritt "frisches" Öl von der linken Seite in das Rohr ein. Infolgedessen sinkt die Öltemperatur an der linken Seite (graue Temperaturkurve) des Rohrs auf Tanktemperaturniveau. Die Austrittstemperatur (blaue Kurve) auf der rechten Seite des Rohrs nähert sich einem konstanten Niveau, wenn das erste Frischöl (das zu Beginn des Ölflusses auf der linken Seite des Rohrs eingetreten ist) das gesamte Rohr durchlaufen hat.

Wärmeübertragung mit zeitlich veränderlichen Wärmeübergangskoeffizienten

Beim zweiten Rohr übersteuert die Eingabe für den externen Wärmeübergangskoeffizienten den parametrisierten Wert und der extern bereitgestellte Wert wird für die Berechnung verwendet. In der ersten Sekunde der Simulation wird der externe Wärmeübergangskoeffizient auf Null gesetzt. Wenn die viskose Erwärmung aufgrund der Flüssigkeitsreibung vernachlässigbar ist, bleibt die Temperatur der Flüssigkeit unverändert.

Nach 2 Sekunden wird der externe Wärmeübergangskoeffizient auf den Standardwert gesetzt (rote Kurve in der unteren Abbildung). Aufgrund der höheren Umgebungstemperatur kommt es nun zu einem positiven Wärmestrom durch die Rohrwand in das Öl, und die rote Temperaturkurve in der oberen Abbildung steigt an. Die Temperatur erreicht das gleiche Beharrungsniveau wie beim Standardrohr, nachdem das erste Frischöl (das nach der Einstellung des Wärmeübergangskoeffizienten auf der linken Seite des Rohrs eingetreten ist) das gesamte Rohr durchquert hat.

Wärmeübertragung mit aufgezwungenem zeitlich veränderlichem Wärmestrom

Das dritte Rohr verwendet den Eingang für den externen Wärmestrom - die Wärmeübergangskoeffizienten werden ignoriert. Positive (Heizung) und negative (Kühlung) Wärmeströme sind zulässig. Ein negativer Wärmestrom hat eine kühlende Wirkung auf die Flüssigkeitstemperatur.

In den ersten 4 Sekunden der Simulation wird der externe Wärmestrom auf Null gesetzt. Nach 4 Sekunden wird der externe Wärmestrom auf den Wert gesetzt, der in der grünen Kurve in der unteren Abbildung dargestellt ist. Dieser Wert wird durch Multiplikation des Wärmedurchgangskoeffizienten U mit der inneren Oberfläche des Rohrs und der logarithmischen durchschnittlichen Temperaturdifferenz zwischen Öl und Umgebung berechnet. Auch hier erreicht die Temperatur ein gleichmäßiges Niveau, wenn das erste Frischöl, das auf der linken Seite des Rohrs eingetreten ist (nachdem der Wärmestrom eingeschaltet wurde), das gesamte Rohr durchlaufen hat.