Die Womersley-Zahl: Grundlagen und Anwendung im Kontext fluidtechnischer Systeme

Die Womersley-Zahl (Wo) ist eine dimensionslose Kennzahl in der Strömungsmechanik, die das Verhältnis zwischen trägheitsbedingten und viskosen Kräften in oszillierenden Strömungen beschreibt. Sie ist besonders relevant für die Analyse von unsteady (zeitlich veränderlichen) Strömungen in Rohrleitungssystemen, wie sie in hydraulischen und pneumatischen Anwendungen auftreten.

Anwendungsbeispiele in der Simulation von Rohrleitungssystemen

Dynamische Strömungen in pulsierenden Systemen
In vielen fluidtechnischen Systemen, beispielsweise in hydraulischen Antrieben oder Pulsationsdämpfern, treten periodische Druck- und Durchflussschwankungen auf. Die Womersley-Zahl hilft dabei, zu bestimmen, ob eine Strömung eher durch Trägheitskräfte oder durch viskose Effekte dominiert wird.
Analyse von Wechselwirkungen in flexiblen Leitungssystemen
In Systemen mit schnell wechselnden Druckverhältnissen, wie etwa in Kraftstoffleitungen oder Blutgefäßen in der Medizintechnik, spielt die Womersley-Zahl eine entscheidende Rolle bei der Vorhersage von Wand-Wechselwirkungen und Druckverlusten.
Optimierung von Rohrleitungssystemen
Bei der Simulation ermöglicht die Berücksichtigung der Womersley-Zahl eine realistischere Modellierung von unsteady Strömungen, was insbesondere in hochfrequenten Systemen mit schnellen Druckänderungen relevant ist. Dadurch lassen sich Druckverluste, Schwingungen und Effizienzverluste genauer analysieren und optimieren.

Die Womersley-Zahl ist ein wichtiges Werkzeug für die Analyse und Simulation zeitlich variabler Strömungen in fluidtechnischen Systemen. Ihre Anwendung in 1D-CFD-Simulationen wie in DSHplus ermöglicht eine detaillierte Bewertung dynamischer Effekte und trägt zur optimierten Auslegung von Rohrleitungssystemen bei.

Theoretischer Hintergrund

Die nach dem britischen Mathematiker John R. Womersley benannte Womersley-Zahl $Wo$ gibt das Verhältnis von Trägheits- zu Zähigkeitskräften bei harmonisch oszillierenden Rohrströmungen an:

$$Wo = \frac{d}{2}\sqrt{\frac{\omega}{\nu}}.$$

Die radiale Verteilung der axialen Geschwindigkeit in der Rohrleitung wird bei oszillierender Rohrströmung stark von der Womersley-Zahl beeinflusst.

Für eine gegebene Volumenstromwellenstärke $\delta Q$ ergibt sich das Geschwindigkeitsprofil nach der folgenden Vorschrift:

$$\delta u(r,t) = \frac{\delta Q}{A}\frac{I_0(R_a) - I_0(R)}{I_2(R_a)}\mathrm{e}^{i\omega t}$$

Dabei bezeichnet $A$ den durchströmten Querschnitt des Rohres, $I_n(x)$ die modifizierte Besselsche Funktion erster Art und $n$-ter Ordnung und $R$ die mit der Kreisfrequenz $\omega$ und der kinematischen Viskosität $\nu$ dimensionslos gemachte Radialkoordinate. Die dimensionslose Radialkoordinate lässt sich durch die Womersley-Zahl ausdrücken:

$$R = r\sqrt{\frac{i\omega}{\nu}} = \frac{r}{r_a}Wo\sqrt{i}$$

Der Einfluss der Womersley-Zahl auf das Geschwindigkeitsprofil ist in der folgenden Abbildung visualisiert:

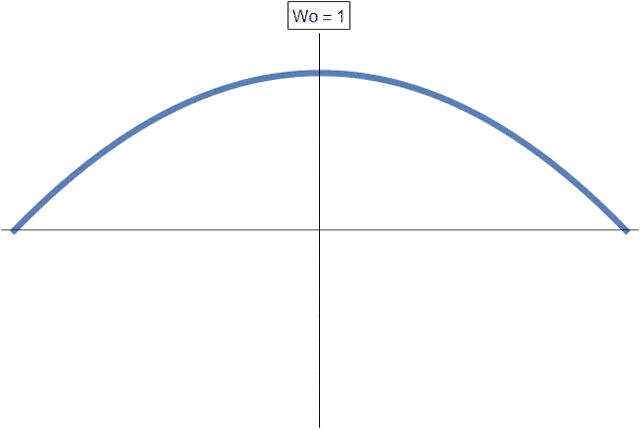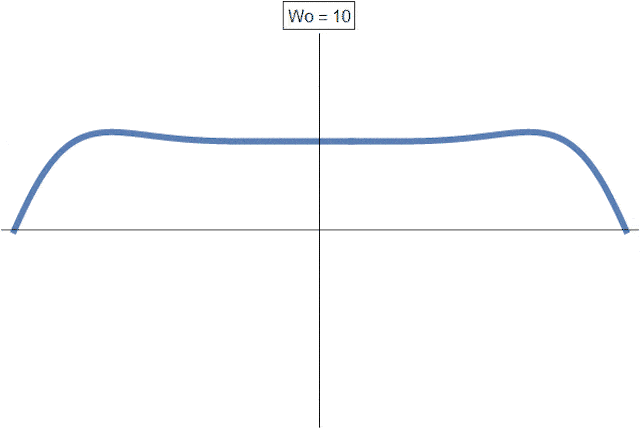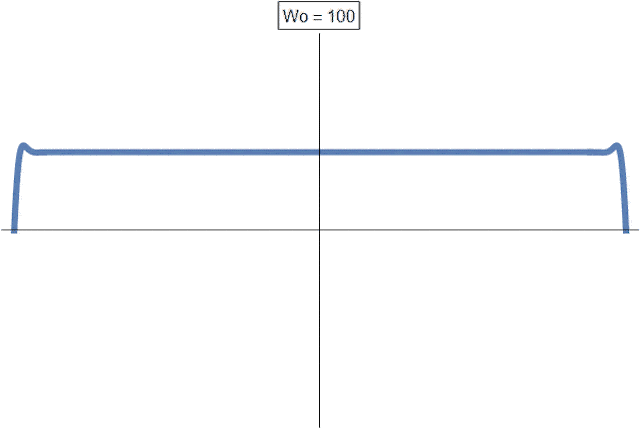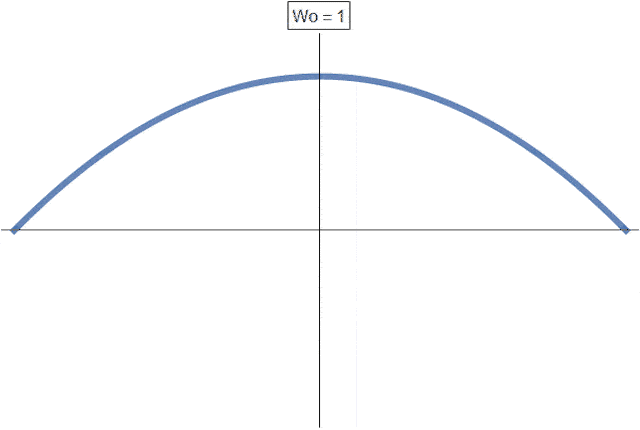
Für sehr kleine Womersleyzahlen geht das Geschwindigkeitsprofil in die aus der stationären Rohrströmung bekannte POISEUILLE-Parabel über. Mit zunehmender Womersley-Zahl (entspricht einer bei ansonsten unverändertem Versuchsaufbau größer werdenden Frequenz $\omega$) wird das Geschwindigkeitsprofil fülliger. Für sehr große Womersley-Zahlen können in Wandnähe Geschwindigkeitsspitzen beobachtet werden, die der Kernströmung vorauseilen. Dieses Phänomen wird in der Literatur als der Richardsonsche Annulareffekt bezeichnet.

Wissenswertes

Da die Womersley-Zahl auch als Reynoldszahl für instationäre Strömungen interpretiert werden kann, ist die Bezeichnung dynamische Reynoldszahl ebenfalls gebräuchlich. Die ebenfalls zur Charakterisierung des Frequenzeinflusses verwendete Valensi-Zahl $Va$ entspricht dem Quadrat der Womersley-Zahl.