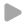Theoretischer Hintergrund & Modellierung in DSHplus
Die verschiedenen Kavitationsformen werden durch geeignete mathematische Modelle in der Simulationsumgebung DSHplus abgebildet.
Auf dieser Seite erfahren Sie, wie...
- Dampfkavitation
- das druckabhängige Gaslösevermögen der Flüssigkeit
- die Aus- und Rücklösegeschwindigkeiten der Gasanteile
- der Gastransport mit der Strömung
- der Einfluss der endlichen Gasanteile auf Stoffdaten
- das „Choking“ in Widerständen
- die Gasauslösung in Widerständen
...in DSHplus modelliert ist.
Im nebenstehenden (englischsprachigen) Video finden Sie den Inhalt dieser Seite als Webinar.
Dampfkavitation
Die Berechnung der Dampfkavitation innerhalb der Rohre basiert auf dem „Discrete Vapor Cavity Model“ (DVCM). Dieses ist das am häufigsten verwendete Modell für die 1D-Berechnung von Strömungen mit Dampfkavitation.
Zugrundeliegende Annahmen:
- Sofortige Umwandlung von Flüssigkeit in Dampf, sobald der Dampfdruck erreicht ist
- Die räumlichen Dimensionen der Dampfblasen sind für die Analyse vernachlässigbar
- Die Dampfblasen werden nicht transportiert
- Die Kavitation wird als isothermer Prozess modelliert, da die Masse der verdampften Phase sehr klein ist.
Berechnungsroutine:
- Berechnung der aktuellen Werte für Druck und Geschwindigkeit am Gitterpunkt i wie bei kavitationsfreier Strömung
- Fällt der Druck unter den Dampfdruck, wird er auf diesem Wert „festgehalten“.
- Aufbauend auf dem vorgeschriebenen Dampfdruck werden die Geschwindigkeiten u1 und u2 berechnet
- Die Differenz zwischen den beiden Geschwindigkeiten entspricht der zeitlichen Änderung des Dampfvolumens Vv
- Der volumetrische Dampfanteil αD ergibt sich aus dem Quotienten von Dampfvolumen Vv und Kontrollvolumen Vi.
Vorteil des DVCM-Modells: Zur Parametrierung wird nur der temperaturabhängige Dampfdruck der Flüssigkeit benötigt!
Druckabhängiges Gaslösevermögen der Flüssigkeit
Die Fähigkeit einer Flüssigkeit, ein Gas zu lösen, wird durch den Bunsen-Koeffizienten αB charakterisiert.
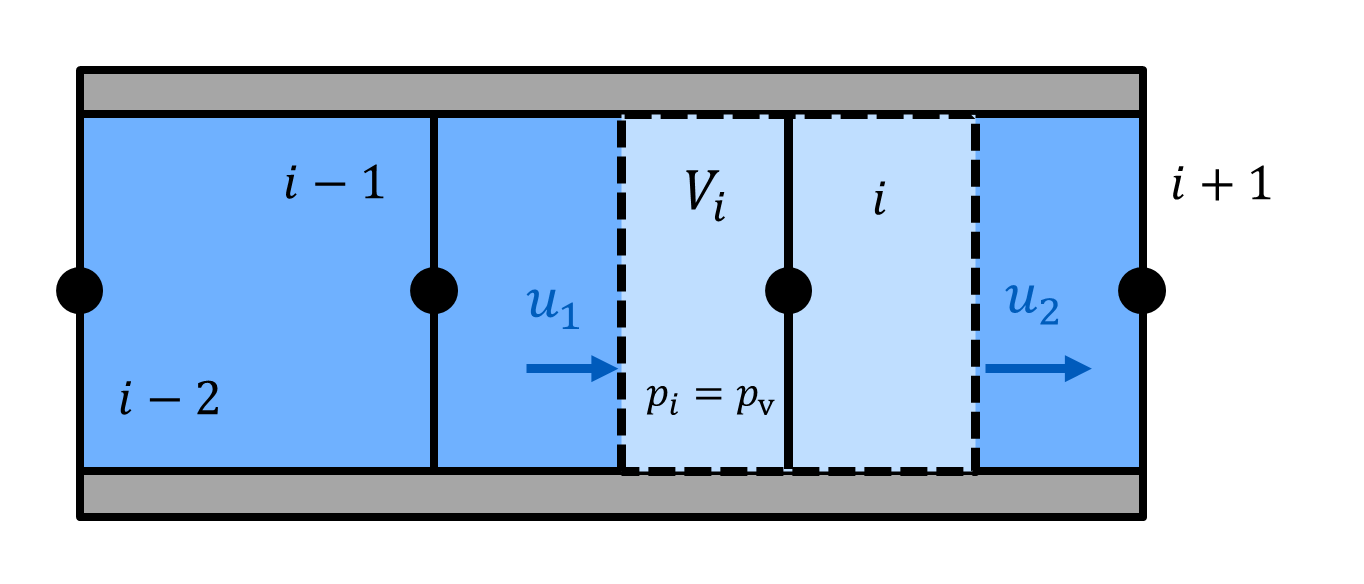
Der Bunsen-Koeffizient gibt an, wie viel Gasvolumen Vdiss0 von einem Flüssigkeitsvolumen VL bei Umgebungsdruck p0 absorbiert werden kann.
Das Gaslösevermögen der Flüssigkeit ist druckabhängig (Henry-Dalton-Gesetz). Für Drücke p ≠ p0 ist das lösbare Gasvolumen durch folgenden Ausdruck gegeben:
$$V_\mathrm{diss0} = \frac{p}{p_0}\alpha_\mathrm{B}V_\mathrm{L}$$
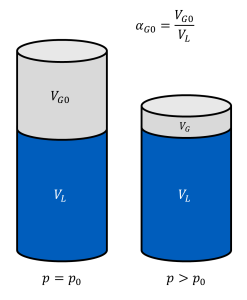
Bei einem Kolben, der mit Hydraulikflüssigkeit und ungelöstem Gas gefüllt ist, wird daher das Volumen VG des ungelösten Gases mit steigendem Druck abnehmen, selbst wenn das Gas inkompressibel wäre (siehe nebenstehende Abbildung)!
Wenn der Volumenanteil des ungelösten Gases bei Umgebungsdruck als αG0 bezeichnet wird, kann der Anteil αG(p) des ungelösten Gases bei einem beliebigen Druck p folgendermaßengegeben berechnet werden (αG bezieht sich dabei immer noch auf die Umgebungsbedingungen!):
$$\alpha_\mathrm{G}(p) = \alpha_\mathrm{G0}+\alpha_\mathrm{B}\left(1-\frac{p}{p_0}\right)$$
Erhöht man den Druck, so geht das Gas oberhalb eines Drucks pα vollständig in Lösung, sodass der Anteil ungelöster Luft αG(p) gleich Null wird:
$$p_\alpha = p_0 \left(1+\frac{\alpha_\mathrm{G0}}{\alpha_\mathrm{B}}\right)$$
Das skizzierte Verhalten lässt sich jedoch nur bei quasi-statischen (sehr langsamen) Druckänderungen beobachten.
Aus- und Rücklösegeschwindigkeiten der Gasanteile
Bei schnellen Druckänderungen müssen die endlichen Absorptions- und Desorptionsraten der Gasanteile berücksichtigt werden!
Das zeitliche Absorptions- bzw. Desorptionsverhalten des Flüssigkeit-Gas-Gemischs wird als ein Verzögerungselement 1. Ordnung (PT1) an den inneren Gitterpunkten des Rohres modelliert.
Die Parameter der Absorptions- und Desorptionsfunktionen (Zeitkonstanten τAbs und τDes) sind systemspezifisch und müssen experimentell bestimmt werden; die Standardparameter von DSHplus liefern eine grobe Orientierung, falls keine Werte bekannt sind.
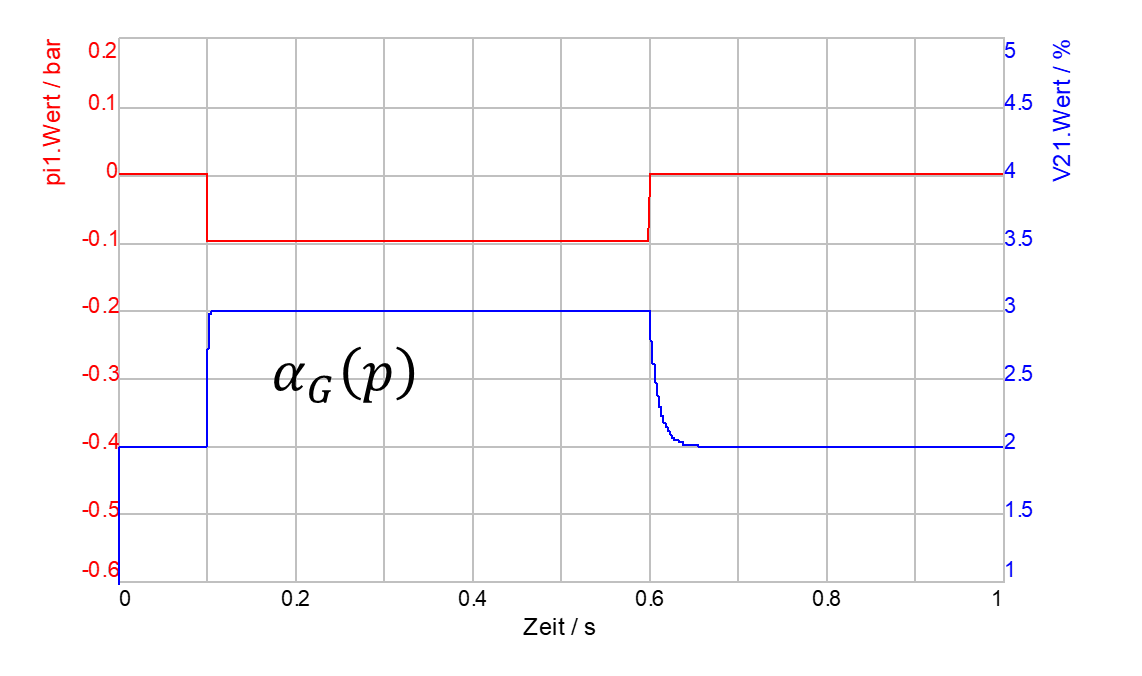
Die Auswirkungen der zeitabhängigen Absorptions- bzw. Desorption sind für beispielhaft gewählte Parameter (τAbs =10 ms, τDes =1 ms) im nebenstehenden DSHplus-Screenshot dargestellt.
Es zeigt sich, dass (entsprechend der Parametrierung) der Anteil ungelösten Gases bei einer Druckabsenkung schnell ansteigt (Desorption), das Rücklösen des Gases bei erneutem Druckanstieg jedoch mit einiger Verzögerung erfolgt.
Gastransport mit der Strömung
Es wird ein homogenes Gemisch angenommen, d. h. gelöste und ungelöste Gasanteile werden mit Fluidgeschwindigkeit transportiert.
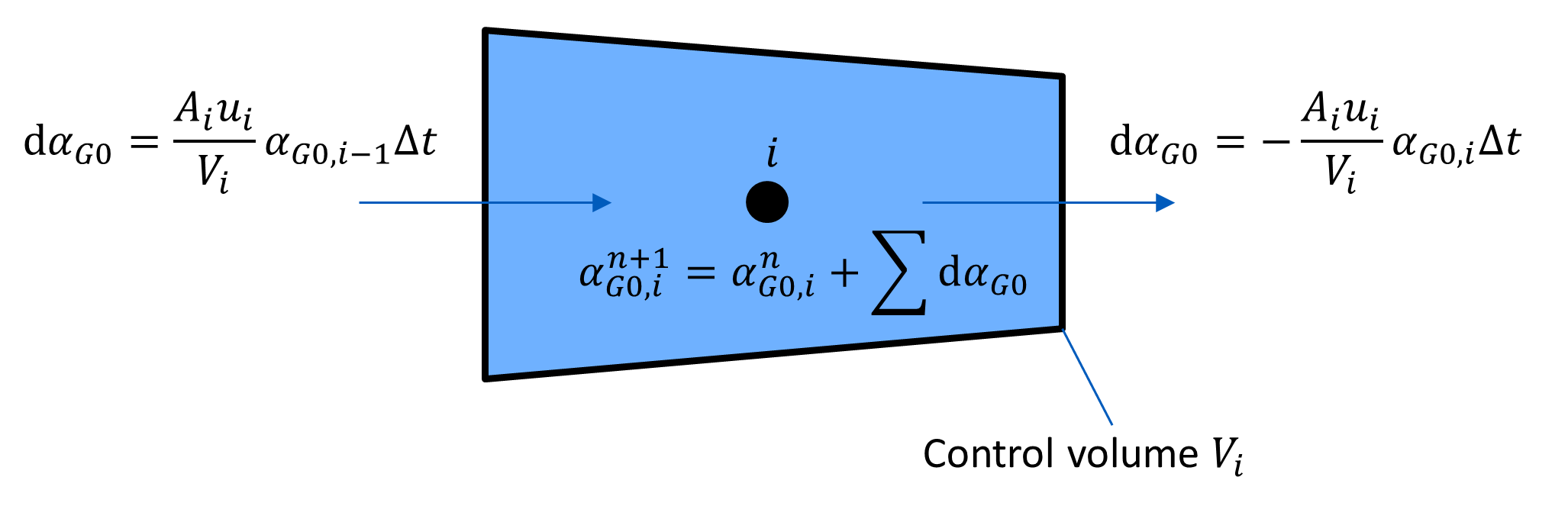
Jedem Gitterpunkt des MOC-Gitters entspricht ein Kontrollvolumen Vi.
Der Gasmassenanteil (oder der äquivalente Anteil des ungelösten Gases αG0 bei Referenzdruck p0) zum neuen Zeitpunkt n+1 wird aus dem einströmenden und ausströmenden Gemischströmen mit ihren entsprechenden Gasmassenanteilen berechnet.
Einfluss endlicher Gasanteile auf Stoffeigenschaften
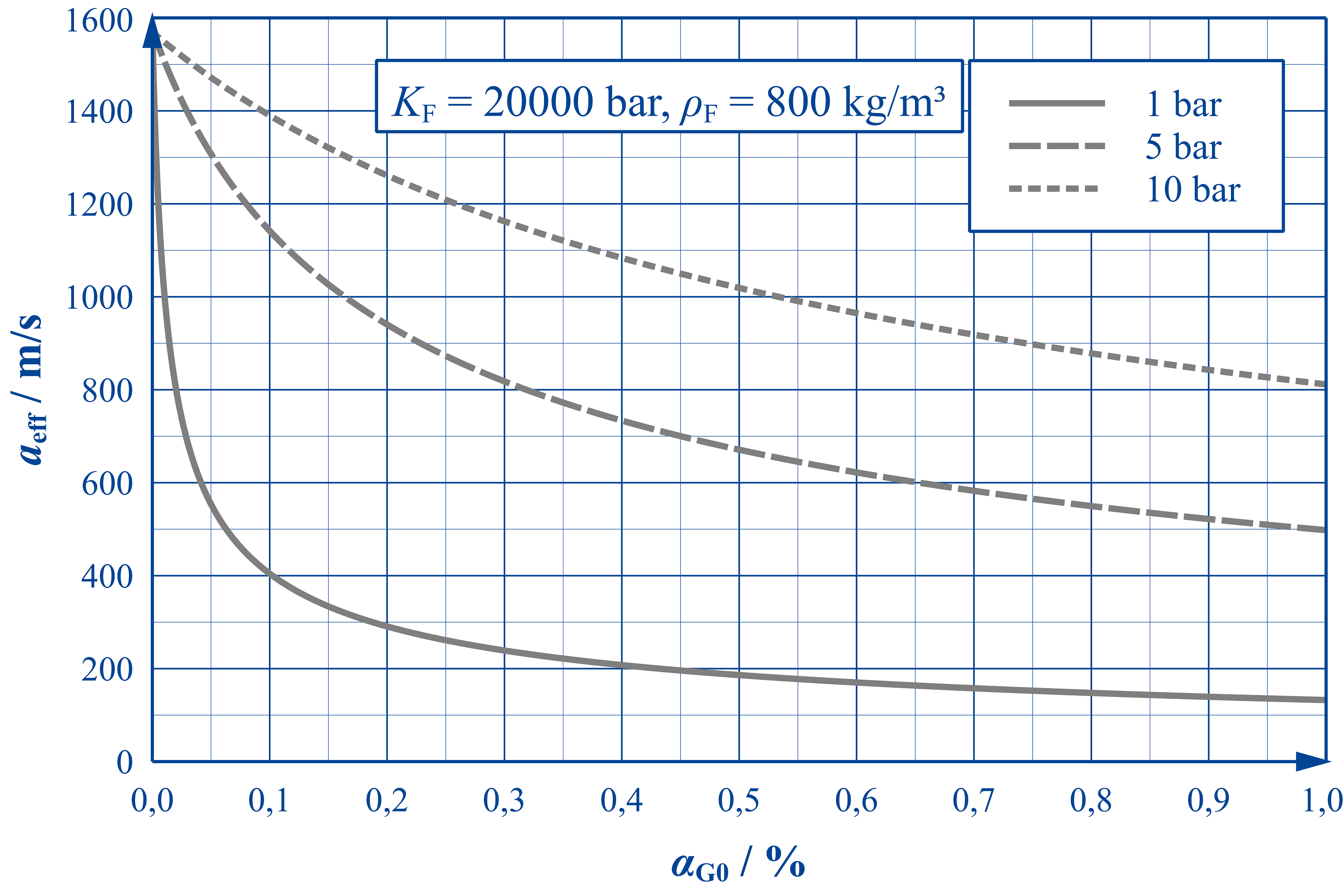
Wo Gasblasen auftreten, erfahren die Eigenschaften der hydraulischen Flüssigkeit (genauer: des Flüssigkeits-Gas-Gemischs) starke Änderungen. Da sich die Gasphase wesentlich leichter als die flüssige Phase komprimieren lässt, fällt die Steifigkeit des Gemischs – charakterisiert durch den effektiven Kompressionsmodul Keff oder die effektive Schallgeschwindigkeit aeff – deutlich geringer als die der „reinen“ Flüssigkeit aus.
Wie die nebenstehende Abbildung zeigt, vermögen selbst geringste Volumenanteile von ungelöster Luft die Schallgeschwindigkeit in Hydraulikölen drastisch zu reduzieren. Mit zunehmendem Druckniveau nimmt der Einfluss der ungelösten Luft ab, da die Blasensteifigkeit proportional zum Druck ansteigt.
Die dargestellten Kurvenverläufe sind nur für langsam ablaufende Prozesse gültig. Bei hochdynamischen Vorgängen (z. B. Druckstößen) muss zusätzlich die Frequenzabhängigkeit der Gasblasensteifigkeit berücksichtigt werden. Diese kann – je nach Frequenzlage – die Steifigkeit des Gemischs weiter absenken oder sogar erhöhen.
„Choking“ in Widerständen
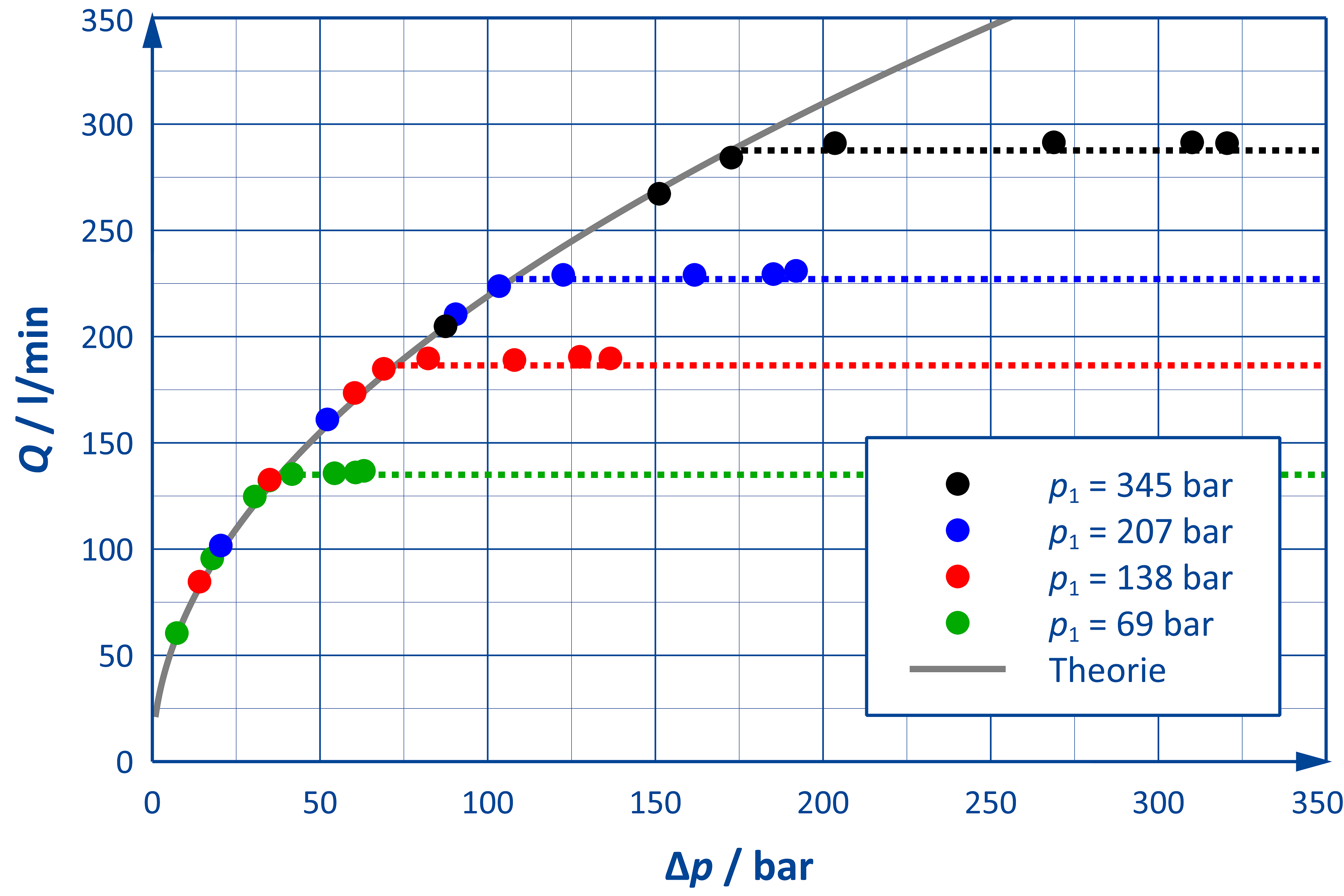
Im Allgemeinen nimmt der Volumenstrom über einen Widerstand mit steigender Druckdifferenz zu. Dies gilt jedoch nur, solange keine Kavitation in der Strömung auftritt. Wird der Dampfdruck unterschritten, kommt es zur Dampfbildung – je mehr Dampf entsteht, umso stärker wird der Durchfluss durch den Widerstand behindert. Es kommt zu einer „Sättigung“ des Volumenstroms – eine größere Druckdifferenz führt nicht mehr zu einer Zunahme des Durchflusses.
Man könnte vermuten, dass die Druckdifferenz über den Widerstand der einzige Parameter ist, der Beginn und Ausmaß der Kavitation bestimmt. Da sich jedoch – wie in der nebenstehenden Abbildung dargestellt – durch Erhöhung des Vordrucks das Auftreten von Kavitation verzögern lässt, kann diese Größe nicht der einzig relevante Parameter sein [1]. Die kombinierten Auswirkungen dieser beiden „Stellschrauben“ werden in der Praxis daher durch den Kavitationsindex C (oder dessen Kehrwert) erfasst [1]:
$$C=\frac{p_1-p_\mathrm{v}}{p_1-p_2}$$
Kleinere Werte des Kavitationsindexes C machen das Auftreten von Kavitation wahrscheinlicher. Kavitation tritt dann auf, wenn der Kavitationsindex unter einen komponentenspezifischen kritischen Wert Ckrit fällt.
Die von EBRAHIMI et al. [1] veröffentlichten Messwerte lassen sich mit einem für die verwendete Ventilart typischen Wert für Ckrit in der 1D-Simulation mit hoher Genauigkeit reproduzieren (gestrichelte Kurven in der nebenstehenden Abbildung).
Gasauslösung in Widerständen
Wenn Kavitation an einem Widerstand auftritt und die Flüssigkeit gelöstes Gas enthält, wird eine bestimmte Menge des Gases freigesetzt.
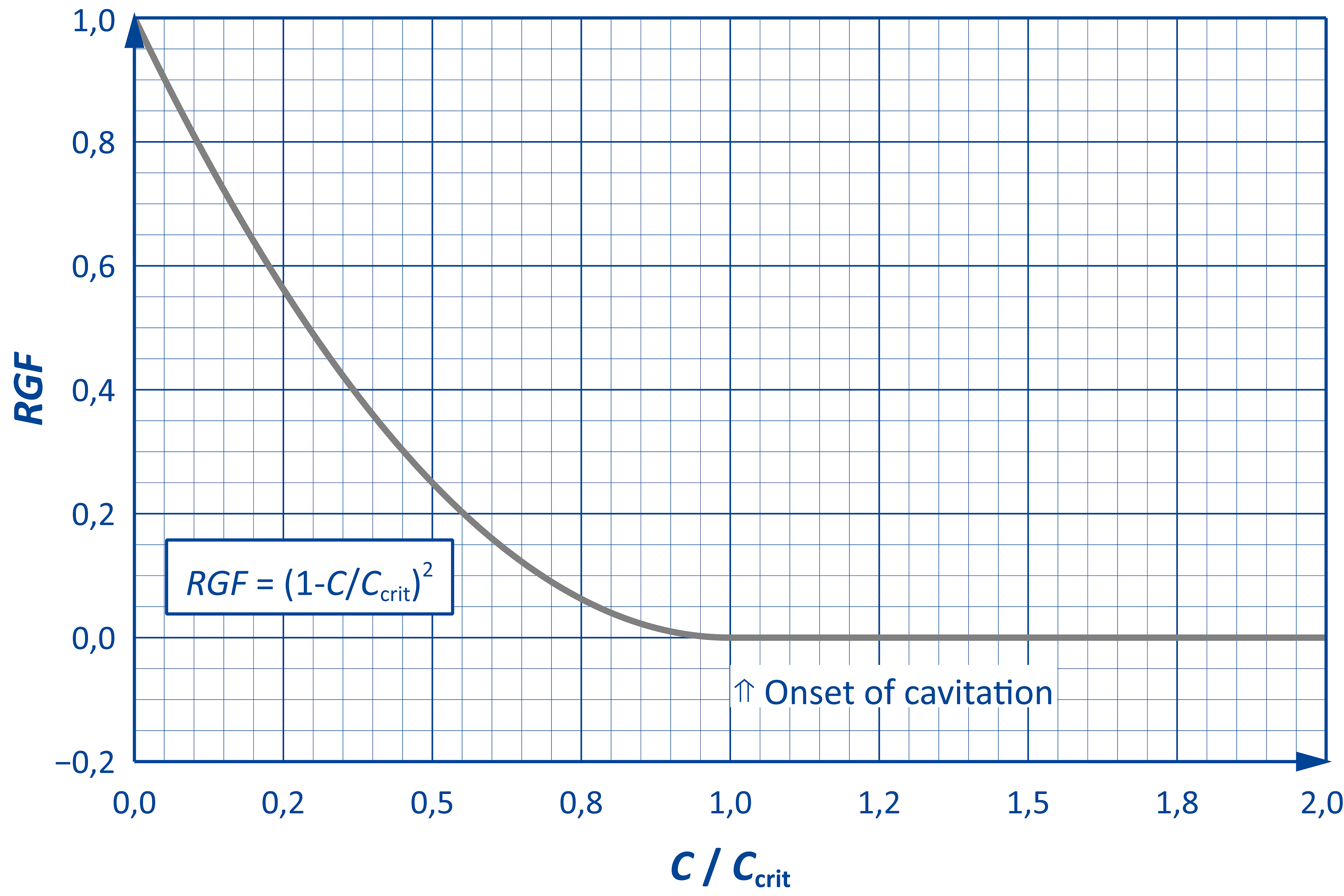
Die durch Kavitation freigesetzte Gasmenge wird durch den freigesetzten Gasanteil RGF beschrieben, der wie folgt definiert ist:
$$RGF=\frac{\mathrm{Released\,volume\,fraction\,of\,gas}}{\mathrm{Incoming\,dissolved\,volume\,fraction\,of\,gas}}$$
Wenn das gesamte Gas im Widerstand freigesetzt wird, nimmt RGF einen Wert von Eins an.
Da die Beziehung zwischen der Geometrie des Widerstandes, dem Druckverlust und dem freigesetzten Gasanteil im Allgemeinen komplex und situationsspezifisch ist, müssen die entsprechenden Werte entweder durch ein Experiment oder durch numerische 2D/3D-Simulationen ermittelt werden.
Um – falls keine Daten verfügbar sind – eine grobe Parametrierung zu ermöglichen, steht in DSHplus ein vorparametriertes, semi-empirisches Modell zur Verfügung (siehe nebenstehende Abbildung).
Literatur
[1] EBRAHIMI, B. et al. „Characterization of high-pressure cavitating flow through a thick orifice plate in a pipe of constant cross section.“ International Journal of Thermal Sciences 114 (2017): 229-240.